Select your current type (AC – Single phase or AC – Three phase), input the real power in kilowatts, the current in amps, the voltage in volts, the frequency in hertz, and the corrected power factor. Click the “Calculate” button to see the power factor result, apparent power, reactive power, and the required correction capacitor value.
Like this? Please share:
How Do I Calculate Power Factor?
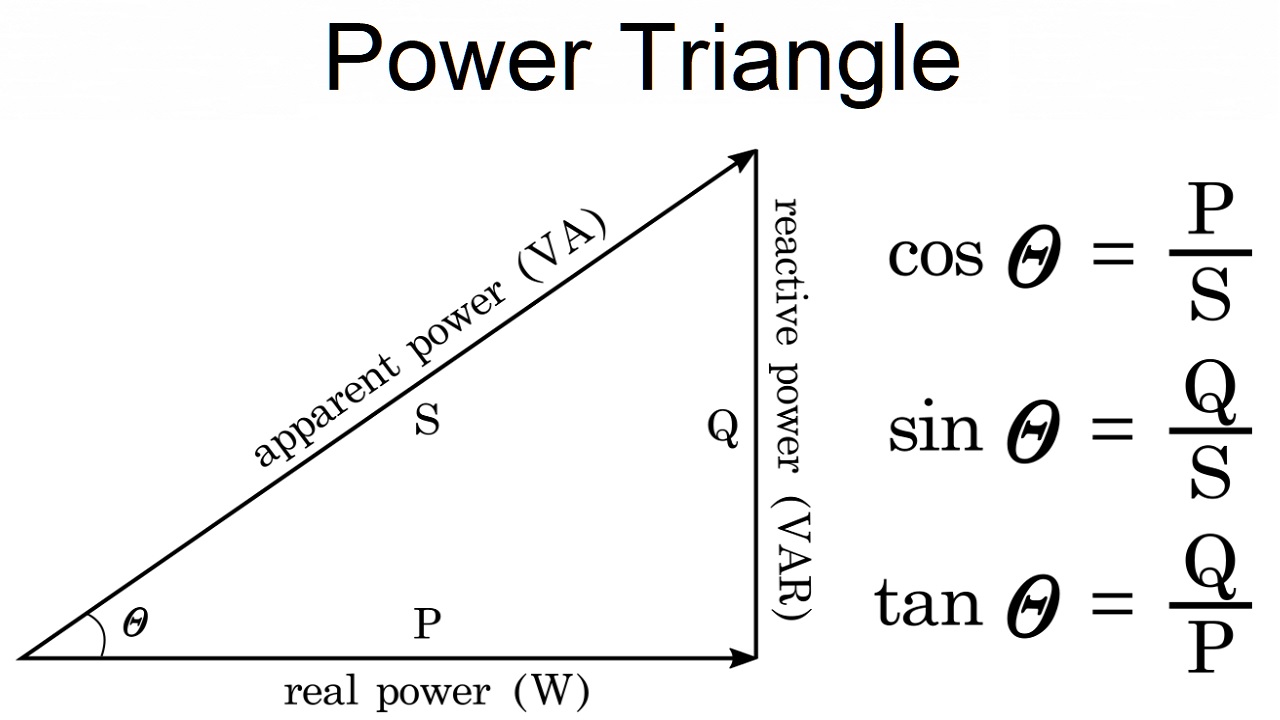
The power factor (PF) is calculated using the formula:
PF = cos θ = Real Power (kW) ÷ Apparent Power (kVA) = P ÷ S [1]
For a single-phase AC system, apparent power S(kVA) is calculated as:
S(kVA) = (V × A) ÷ 1000 [2]
For a three-phase system with line-to-line voltage, it is:
S(kVA) = (3 × V × A) ÷ 1000 [3]
For a three-phase system with line-to-neutral voltage, it is:
S(kVA) = (3 × V × I) ÷ 1000 [4]
To correct the power factor, the required correction capacitor (C) is calculated using:
CµF = Qc × 109 ÷ (2 × π × f × V2), where f is the frequency in hertz, π is the mathematical constant and V is the voltage in volts [5].
The reactive power compensation Qc is calculated as the difference between the initial reactive power (Q) and the corrected reactive power (Qcorrected):
Qc = Q − Qcorrected [6]
Q is the initial reactive power, calculated as:
Q(kVAR) = (S)2 − (P)2 [7]
Qcorrected is the corrected reactive power, calculated as:
Qcorrected (kVAR) = (Scorrected)2 − (P)2 [8]
Corrected apparent power Scorrected:
Scorrected (kVA) = P(kW) ÷ PFcorrected [9]
Real Calculation Example
Let’s consider a household appliance operating in a single-phase AC circuit. Suppose the appliance has a real power consumption of 3 kW, the current is 15 amps, the voltage is 230 volts, and the frequency is 50 Hz. The corrected power factor is 0.9.
First, calculate the apparent power:
S = V × I = 230V × 15A = 3450 VA = 3.45 kVA
Then, calculate the initial power factor:
PF = P ÷ S = 3 kW ÷ 3.45 kVA ≈ 0.87
To correct the power factor to 0.9, determine the corrected apparent power:
Scorrected = PCorrected ÷ PF = 3 kW ÷ 0.9 ≈ 3.3333 kVA
Next, calculate the initial reactive power:
Q = (S)2 − (P)2 = (3.45)2 − (3)2 = 1.7037 kVAR
And the corrected reactive power:
Qcorrected = (Scorrected)2 − (P)2 = (3.3333)2 − (3)2 = 1.4529 kVAR
Finally, determine the reactive power that needs correction:
Qc = Q − Qcorrected = 1.7037 − 1.4529 = 0.2508 kVAR
Calculate the required capacitance for correction:
C = 109 × Qc ÷ (2 × π × f × V2) = 109 × 0.2508 ÷ (2 × 3.14159 × 50 * 2302) = 250800000 ÷ 16619011.1 ≈ 15.09 μF
References
- https://en.wikipedia.org/wiki/Power_factor
- Ewald Fuchs; Mohammad A. S. Masoum (14 July 2015). Power Quality in Power Systems and Electrical Machines. Elsevier Science. pp. 432–. ISBN 978-0-12-800988-8. “
The DPF is the cosine of the angle between these two quantities
“.
